The quantity 0.4444444444444444444444444 as a fraction is a repeating decimal that is easy but profound in its mathematical representation. Converting such decimals into fractions not most effective simplifies their use however moreover offers deeper belief into the mathematical relationships they constitute. This article offers an in depth guide to converting this repeating decimal into a fraction and explores its actual-worldwide importance.
What Is 0.4444444444444444444444444?
The number 0.4444444444444444444444444 as a fraction is a habitual decimal in which the digit four repeats infinitely. Represented as:
zero.4‾0.Overlinefour0.Four
This notation suggests that four continues indefinitely after the decimal issue. Such numbers are known as habitual decimals, and they could continually be expressed as fractions.
Step-by way of-Step Conversion of 0.4444444444444444444444444 as a Fraction
Step 1: Assign the Decimal to a Variable
Let’s represent the repeating decimal as:
x=0.Four‾x = zero.Overlinefourx=zero.4
Step 2: Multiply thru 10 to Shift the Decimal Point
To isolate the repeating component, multiply every facets through 10:
10x=four.Four‾10x = 4.Overlinefour10x=4.Four
Step 3: Subtract the Original Equation
Subtract the authentic equation from the new equation:
10x−x=four.4‾−0.Four‾10x – x = 4.Overlinefour – 0.Overlinefour10x−x=four.Four−0.Four
This simplifies to:
9x=49x = 49x=4
Step 4: Solve for x
Divide each sides with the aid of 9:
x=49x = frac49x=90 4
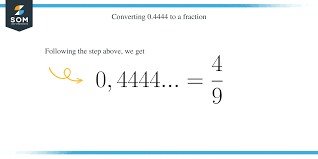
Thus, 0.4444444444444444444444444 as a fraction equals:
49boxedfrac4994Verification of the Result
To verify the accuracy, divide 4 through using 9:
40 9=0.4444444444444444444444444frac49 = 0.444444444444444444444444494=0.4444444444444444444444444 as a fraction
The end result suits the precise decimal, verifying that the fraction 49fracfournine94 is absolutely correct.
Mathematical Insights Into 4/nine
1. Simplified Form
The fraction 49frac4nine94 is in its handiest form because of the fact the numerator (four) and denominator (nine) don’t have any commonplace factors apart from 1.
2. Proper Fraction
Since the numerator is smaller than the denominator, 49fracfournineninety 4 is classed as a proper fraction.
3. Recurring Decimal
When expressed as a decimal, 49frac4nineninety four consequences within the regular decimal zero.Overlinefour.
Applications of 0.4444444444444444444444444 and four/9
1. Probability and Statistics
Fractions like 49frac4nine94 are normally applied in opportunity to represent possibilities or ratios. For example, if there are nine popular consequences and 4 favorable ones, the possibility is 49frac4nineninety four.
2. Financial Calculations
In finance, routine decimals and their fractional equivalents often simplify hobby charge calculations, ratios, and projections.
3. Science and Engineering
In engineering and clinical computations, everyday decimals like 0.Overline4 are frequently converted to fractions for precision in calculations.
General Approach to Converting Repeating Decimals
The approach used to convert 0.4444444444444444444444444 as a fraction into a fragment may be finished to any repeating decimal. Here are a few commonplace examples:
- 0.Overlinethree = 13frac1331
- 0.Overline6 = 23frac2three32
- 0.Overline7 = 79frac7997
By following a scientific approach, any repeating decimal may be represented as a fraction.
Conclusion
The regular decimal 0.4444444444444444444444444 as a fraction is mathematically equal to the fraction 0.4444444444444444444444444 as a fraction. This conversion isn’t always only a mathematical exercising however also a practical tool for simplifying complicated troubles in numerous fields, which consist of opportunity, finance, and engineering. Understanding a way to convert repeating decimals into fractions enhances mathematical fluency and problem-fixing competencies.
Fractions provide a easy and concise way to symbolize routine decimals, imparting precision and readability. By getting to know this method, we can free up new techniques to technique and resolve real-international troubles with self guarantee.